Distance between two points

Cartesian Co-ordinate

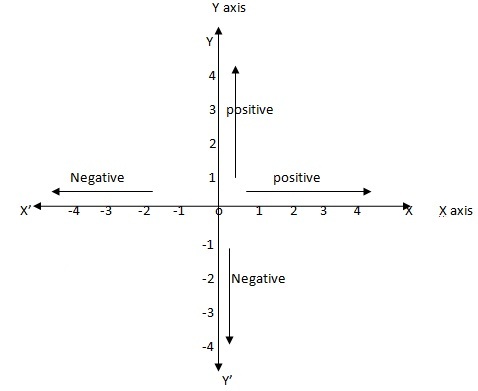
If two perpendicular line passes through any point O then we called point O as origin .in above figure YOY' is perpendicular to XOX' and passes through point O so O is origin and YOY' is called y-axis and XOX' become x-axis. both perpendicular line known as a axis of coordinates. We describe axis as positive and negative From origin O right side line OX is positive and left side line OX' is negative and same rule applied for Y axis from origin O , OY is positive and OY' is known as negative.

Quadrants

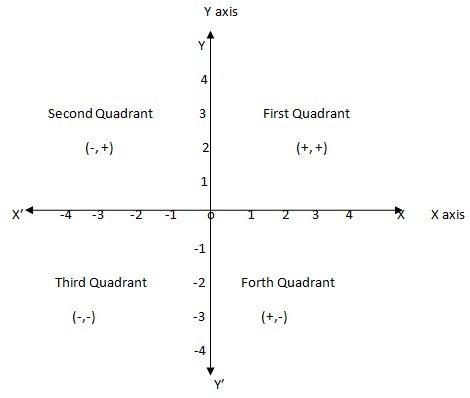
perpendicular line XOX' and YOY' divided the plane into four part that parts are known as quadrants .in the above figure YOX is first quadrant , YOX' is second quadrant,X'OY' is third quadrant and XOY' is known as forth quadrant.

values of x and y in respective to quadrant
First quadrant values x>0 and y>0
Second quadrant values x<0 and y>0
Third quadrant values x<0 and y<0
Forth quadrant values x>0 and y<0
coordinates of origin is always (0,0)

Find points location in coordinates
point P(2,2)
point Q(-5,2)
point R(-4,-5)
points S(3,-7)

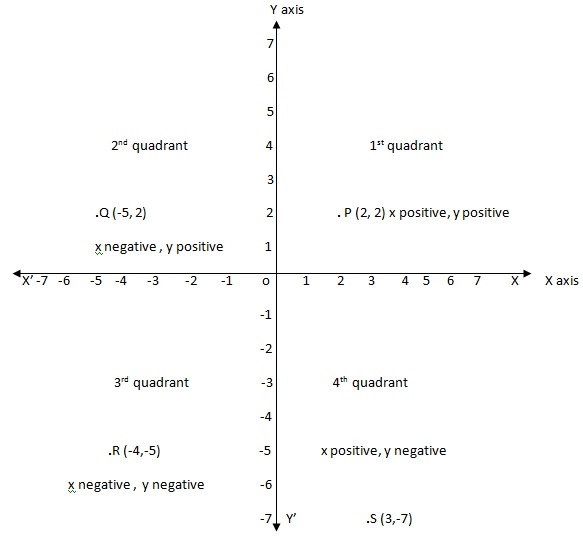
X and Y coordinates of point P is x=2, y=2 both are positive so points lies in first coordinates.
X and Y coordinates of point Q is x=-5, y=2 here x is negative and y is positive so points lies in second coordinates.
X and Y coordinates of point R is x=-4, y=-5 here x is negative and y is also negative so points lies in third coordinates.
X and Y coordinates of point S is x=3, y=-7 here x is positive and y is negative so points lies in forth coordinates.

According to these axis and quadrant we can find location of points for example if any point P(x,y) located in these coordinate and value of x and y is (1,3) both are positive then that points located in first quadrants .

Find distance between points

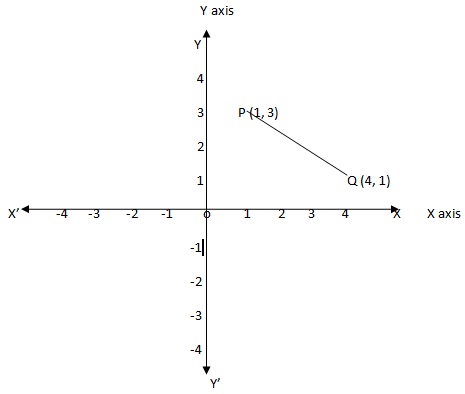
Distance between two points is a length of straight line that use to join both point in plane or quadrants.
in above figure point P(1,3) and point Q(4,1) joining by line PQ so distance between points is length of line PQ.
Formula for finding distance between two point P an Q is:

$$\text{distance PQ}=\sqrt{(x_2-<!--\; -\; -->x_1{)}^2+(y_2-<!--\; -\; -->y_1{)}^2}$$

Put the value of point P(x₁,y₁,) and Q(x₂,y₂) and get distance between point

$$\text{distance of PQ}=\sqrt{(4-<!--\; -\; -->1{)}^2+(1-<!--\; -\; -->3{)}^2}$$ $$\text{distance of PQ}=\sqrt{(3{)}^2+(-<!--\; -\; -->2{)}^2}$$ $$\text{distance of PQ}=\sqrt{9+4}$$ $$\text{distance of PQ}=\sqrt{13}$$